VAE介绍
VAE,即变分自编码器,是常见的生成模型其中一类。常见的生成模型类型还有GAN、flow、DDPM等。
前置知识
1. KL散度
KL散度可以衡量两个分布的相似程度,当KL散度为0时,代表两个分布完全相同。注意KL散度不是距离,因为 KL(p||q)不等于KL(q||p). KL散度的计算公式为:
$$
\begin{align}
KL(p||q)&=\int p(x)\log\frac{p(x)}{q(x)}dx \\
&=\sum_{i=1}^{N}p(x_i)\log{\frac{p(x_i)}{q(x_i)}}
\end{align}
$$
高斯分布的KL散度(公式推导):
$$
KL(N(\mu_1, \sigma_1^2),N(\mu_2, \sigma_2^2))=-\frac{1}{2}+\log(\frac{\sigma_2}{\sigma_1})+\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2}
$$
$$
KL(N(\mu_1, \sigma_1^2),N(0,1))=\frac{1}{2}\left(\mu_1^2+\sigma_1^2-2\log{(\sigma_1)-1}\right)
$$
2. 重参数化技巧
由于直接从$N(\mu,\sigma^2)$的分布中采样对分布的参数是不可导的,因此先从$N(0,1)$采样出 $z$,再得到 $\sigma z+\mu$,这样采样出来对 $\sigma$ 和 $\mu$ 就是可导的。
VAE来龙去脉
1. AE
AE,即自动编码器,由编码器和解码器两部分组成,编码器将输入映射成一种“数值编码”,解码器将“数值编码”映射回图像,这里编码空间是没有任何限制的。如果训练时没有将某个图片编码,那么我们就不太可能生成这个图片。因此,AE适合用于数据压缩和恢复,不太适合于数据生成。
2. VAE
AE离图像生成只差一步了。只要AE的编码空间比较规整,符合某个简单的数学分布(比如最常见的标准正态分布),那我们就可以从这个分布里随机采样向量,再让解码器根据这个向量来完成随机图片生成了。VAE不将输入图片映射成“数值编码”,而将其映射为“分布”,VAE可以生成没有见过的图片。以下是AE和VAE的对比图:

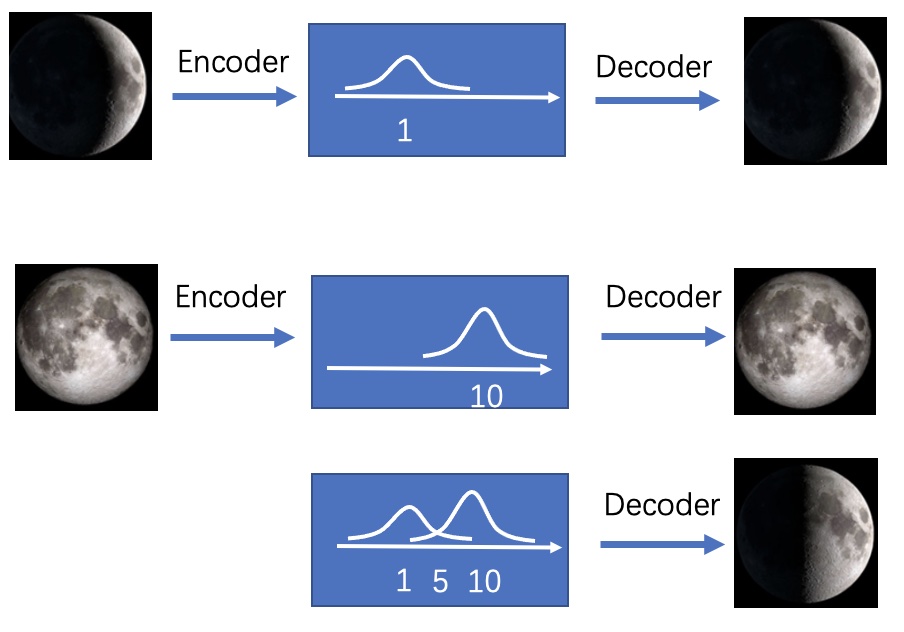
VAE的结构图如下:
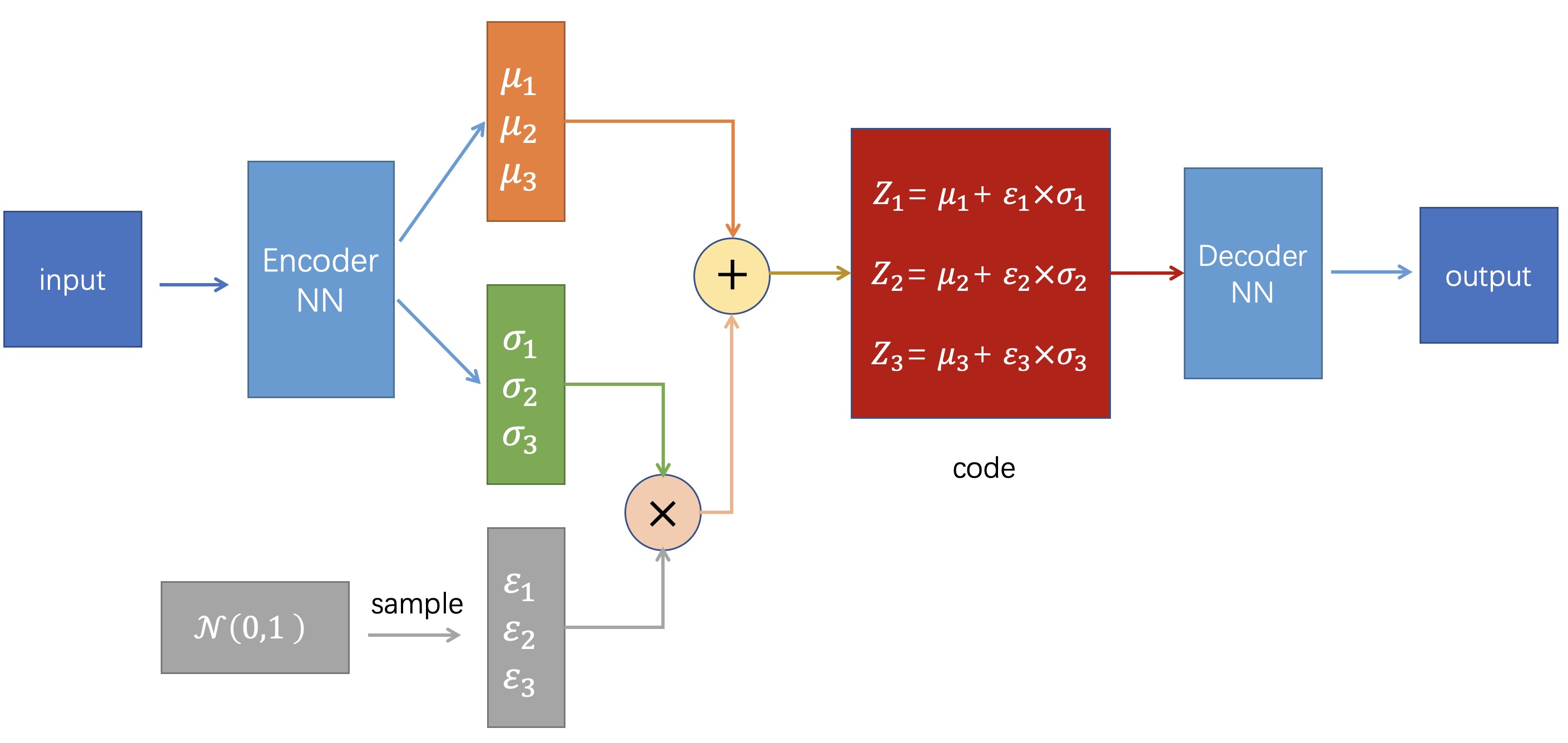
训练VAE时,损失函数包括两部分:
- 为了让输出和输入尽可能像,所以要让输出和输入的差距尽可能小,此部分用MSELoss来计算,即最小化 MSELoss。
- 训练过程中,如果仅仅使输入和输出的误差尽可能小,那么随着不断训练,会使得$\sigma$趋近于0,这样就使得VAE越来越像AE,对数据产生了过拟合,编码的噪声也会消失,导致无法生成未见过的数据。因此为了解决这个问题,我们要对$\mu$和$\sigma$加以约束,使其构成的正态分布尽可能像标准正态分布,具体做法是计算$N(\mu,\sigma^2)$与$N(0,1)$之间的KL散度。
即 $loss = MSE(X, X')+KL(N(\mu, \sigma^2), N(0,1))$,代码如下:
def loss_function(self, recon, x, mu, log_std) -> torch.Tensor:
recon_loss = F.mse_loss(recon, x, reduction="sum") # use "mean" may have a bad effect on gradients
kl_loss = -0.5 * (1 + 2*log_std - mu.pow(2) - torch.exp(2*log_std))
kl_loss = torch.sum(kl_loss)
loss = recon_loss + kl_loss
return loss两部分loss对隐变量z的生成的可视化效果如下图:
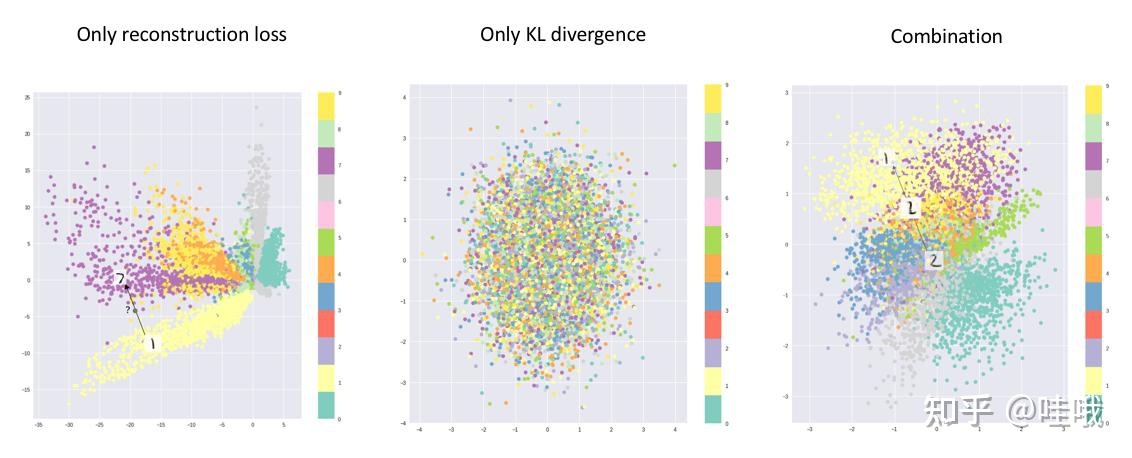
注:VAE的缺点是生成的图像不一定那么“真”,如果要使生成的数据“真”,则要用到GAN。
以上是从直觉方面对VAE损失函数的理解,接下来再从ELBO(Evidence Lower Bound)推导一下,其中$p_\theta$为生成模型,$q_\phi$为推断模型:
$$
\begin{align}
p(x)&=\int p_{\theta}(x|z)p(z) dz \\
p(x)&=\int q_{\phi}(z|x) \frac{p_{\theta}(x|z)p(z)}{q_{\phi}(z|x)} dz \\
\log p(x) &= \log E_{q_\phi(z|x)}\left[\frac{p_{\theta}(x|z)p(z)}{q_{\phi}(z|x)}\right] \\
&\geq E_{q_\phi(z|x)}\left[\log \frac{p_{\theta}(x|z)p(z)}{q_{\phi}(z|x)}\right]
\end{align}
$$
最大化 $\log p(x)$ 可以最大化它的变分下界(ELBO),那么损失函数就是-ELBO:
$$
\begin{align}
loss &= -ELBO \\
&= E_{q_\phi(z|x)}\left[\log q_{\phi}(z|x) - \log p(z) - \log p_{\theta}(x|z) \right] \\
&= E_{q_\phi(z|x)}\left[\log q_{\phi}(z|x) - \log p(z) \right] - E_{q_\phi(z|x)}\left[\log p_{\theta}(x|z) \right] \\
&= KL(q_\phi(z|x)||p(z)) - E_{q_\phi(z|x)}\left[\log p_{\theta}(x|z) \right]
\end{align}
$$
3. CVAE
前面所说的AE适合数据压缩与还原,不适合生成未见过的数据。VAE适合生成未见过的数据,但不能控制生成内容。而CVAE(Conditional VAE)可以在生成数据时通过指定其标签来生成想生成的数据。CVAE的结构图如下所示:

整体结构和VAE差不多,区别是在将数据输入Encoder时把数据内容与其标签(label)合并(cat)一起输入,将编码(Z)输入Decoder时把编码内容与数据标签(label)合并(cat)一起输入。注意label并不参与Loss计算,CVAE的Loss和VAE的Loss计算方式相同。
4. VQ-VAE
VAE生成出来的图片都不是很好看。VQ-VAE的作者认为,VAE的生成图片之所以质量不高,是因为图片被编码成了连续向量。而实际上,把图片编码成离散向量会更加自然。比如我们想让画家画一个人,我们会说这个是男是女,年龄是偏老还是偏年轻,体型是胖还是壮,而不会说这个人性别是0.5,年龄是0.6,体型是0.7。因此,VQ-VAE会把图片编码成离散向量。
把图像编码成离散向量后,又会带来两个新的问题。第一个问题是,神经网络会默认输入满足一个连续的分布,而不善于处理离散的输入。如果你直接输入0, 1, 2这些数字,神经网络会默认1是一个处于0, 2中间的一种状态。为了解决这一问题,我们可以借鉴NLP中对于离散单词的处理方法。为了处理离散的输入单词,NLP模型的第一层一般都是词嵌入层,它可以把每个输入单词都映射到一个独一无二的连续向量上。这样,每个离散的数字都变成了一个特别的连续向量了。
我们可以把类似的嵌入层加到VQ-VAE的解码器前。这个嵌入层在VQ-VAE里叫做"embedding space(嵌入空间)",在后续文章中则被称作"codebook"。
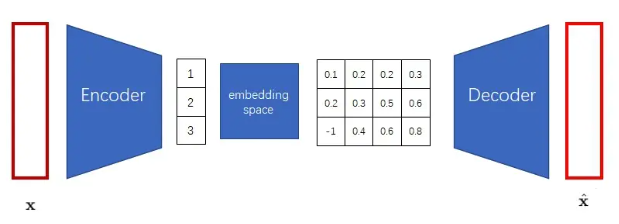
对于VQ-VAE中的细节问题,如VQ-VAE的编码器怎么输出离散向量、VQ-VAE怎么优化编码器和解码器、怎么优化嵌入空间,这里简要说一下,详细见知乎-周奕帆
VQ-VAE输出离散向量,然后又需要Embedding把它映射成特别的连续向量,可以发现这个过程是有冗余的。VQ-VAE的做法是,对于编码器的每个输出向量$z_e(x)$,找到它在嵌入空间的最近邻$z_q(x)$,把$z_e(x)$替换成$z_q(x)$作为解码器的输入。至于这一步怎么算梯度怎么优化,就是前向传播算损失用$z_q(x)$,反向传播传梯度用$z_e(x)$。总的损失包括重建误差+嵌入空间误差。
$$
\begin{align}
L=&\left\|x-\operatorname{decoder}\left(z_{e}(x)+sg(z_{q}(x)-z_{e}(x))\right)\right\|_{2}^{2} \\
+&\alpha\left\|sg(z_{e}(x))-z_{q}(x)\right\|_{2}^{2}+\beta\left\|z_e(x)-sg(z_{q}(x))\right\|_{2}^{2}
\end{align}
$$
为了让梯度从解码器传到编码器,作者使用了一种巧妙的停止梯度算子sg,让正向传播和反向传播按照不同的方式计算。嵌入空间误差为嵌入和其对应的编码器输出的均方误差。为了让嵌入和编码器以不同的速度优化,作者再次使用了停止梯度算子,把嵌入的更新和编码器的更新分开计算。
5. VQ-VAE用于图像生成
离散向量的另一个问题是它不好采样。回忆一下,VAE之所以把图片编码成符合正态分布的连续向量,就是为了能在图像生成时把编码器扔掉,让随机采样出的向量也能通过解码器变成图片。现在倒好,VQ-VAE把图片编码了一个离散向量,这个离散向量构成的空间是不好采样的。没错!VQ-VAE根本不是一个图像生成模型。它和AE一样,只能很好地完成图像压缩,把图像变成一个短得多的向量,而不支持随机图像生成。VQ-VAE和AE的唯一区别,就是VQ-VAE会编码出离散向量,而AE会编码出连续向量。
可为什么VQ-VAE会被归类到图像生成模型中呢?这是因为VQ-VAE的作者利用VQ-VAE能编码离散向量的特性,使用了一种特别的方法对VQ-VAE的离散编码空间采样。VQ-VAE的作者之前设计了一种图像生成网络,叫做PixelCNN。PixelCNN能拟合一个离散的分布。比如对于图像,PixelCNN能输出某个像素的某个颜色通道取0~255中某个值的概率分布。(实际上,PixelCNN不是唯一一种可用的拟合离散分布的模型。我们可以把它换成Transformer,甚至是diffusion模型。)这不刚好嘛,VQ-VAE也是把图像编码成离散向量。换个更好理解的说法,VQ-VAE能把图像映射成一个「小图像」。我们可以把PixelCNN生成图像的方法搬过来,让PixelCNN学习生成「小图像」。这样,我们就可以用PixelCNN生成离散编码,再利用VQ-VAE的解码器把离散编码变成图像。
让我们来整理一下VQ-VAE的工作过程。
- 训练VQ-VAE的编码器和解码器,使得VQ-VAE能把图像变成「小图像」,也能把「小图像」变回图像。
- 训练PixelCNN,让它学习怎么生成「小图像」。
- 随机采样时,先用PixelCNN采样出「小图像」,再用VQ-VAE把「小图像」翻译成最终的生成图像。

