实例分割-PolarMask-CVPR2020
PolarMask是一种基于FCOS的,单阶段的实例分割框架。它首次证明了实例分割的复杂性,无论是网络设计还是计算复杂度,都可以和bbox目标检测相同,并且具有不错的准确性。
论文:PolarMask: Single Shot Instance Segmentation with Polar Representation
代码:https://github.com/xieenze/PolarMask
1. 框架
实例分割mask的表示方式:
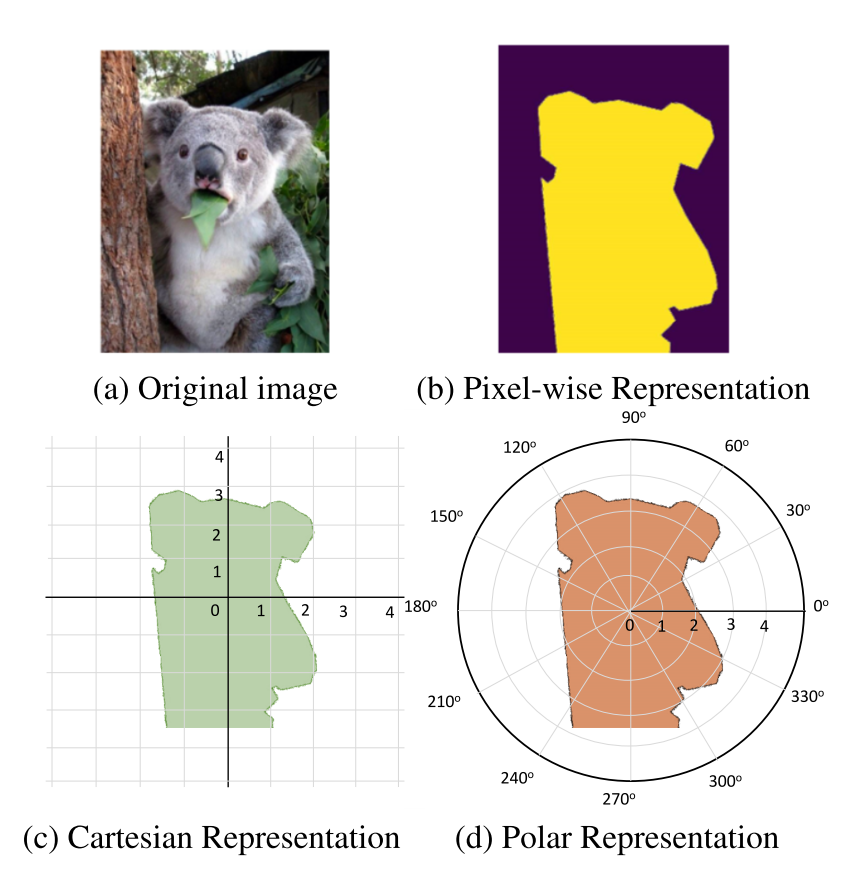
- 像素表示法(图b):对每个像素分类,如Mask R-CNN。
- 轮廓表示法(图c、d):图c中使用轮廓中的点的笛卡尔坐标表示,而本文采用图d所示的极坐标表示,把实例分割问题转化为实例中心点分类(instance center classification)问题和密集距离回归(dense distance regression)问题。
方法的框架如下:
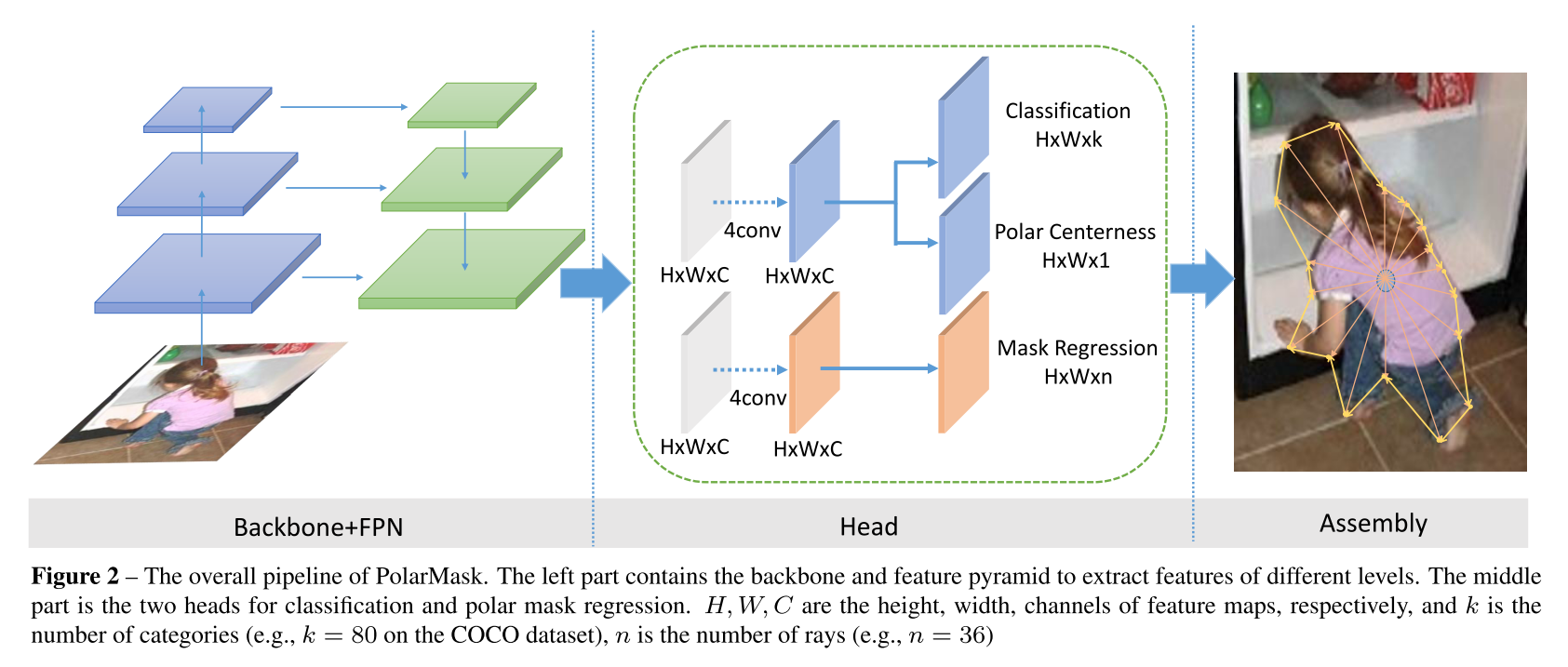
通过backbone和特征金字塔提取特征,头部由中心点分类、Polar Centerness、以及射线长度回归三个分支组成。相比FCOS,只是把FCOS的回归分支的channel=4替换为channel=n, 这里n=36,相当于36根射线的长度。
经过网络,可以得到中心点的位置和类别、n根射线的长度,根据角度和射线长度得到轮廓点的坐标,从0°开始连接这些点,最后得到的连通区域就是实例分割的结果。
2. 实现细节
2.1 target
-
分类分支:实验对比了框中心和质心,选取效果更好的质心。正样本定义为特征图上质心周围1.5倍步长的区域。
-
回归距离:如果一条射线与实例轮廓有多个交点,选最长的一条。如果没有交点,取最小值如$10^{-6}$。
-
Polar Centerness:$\text { Polar Centerness }=\sqrt{\frac{\min \left(\left\{d_{1}, d_{2}, \ldots, d_{n}\right\}\right)}{\max \left(\left\{d_{1}, d_{2}, \ldots, d_{n}\right\}\right)}}$,d为一个实例的n条射线长度。
根据下图可以看到,在实例分割任务中,Polar Centerness比原来FCOS的Centerness定义更好

2.2 Loss
分类分支使用Focal loss,Centerness分支使用交叉熵损失,回归分支使用自己定义的Polar IoU Loss:
首先,极坐标系中的IoU表示为:
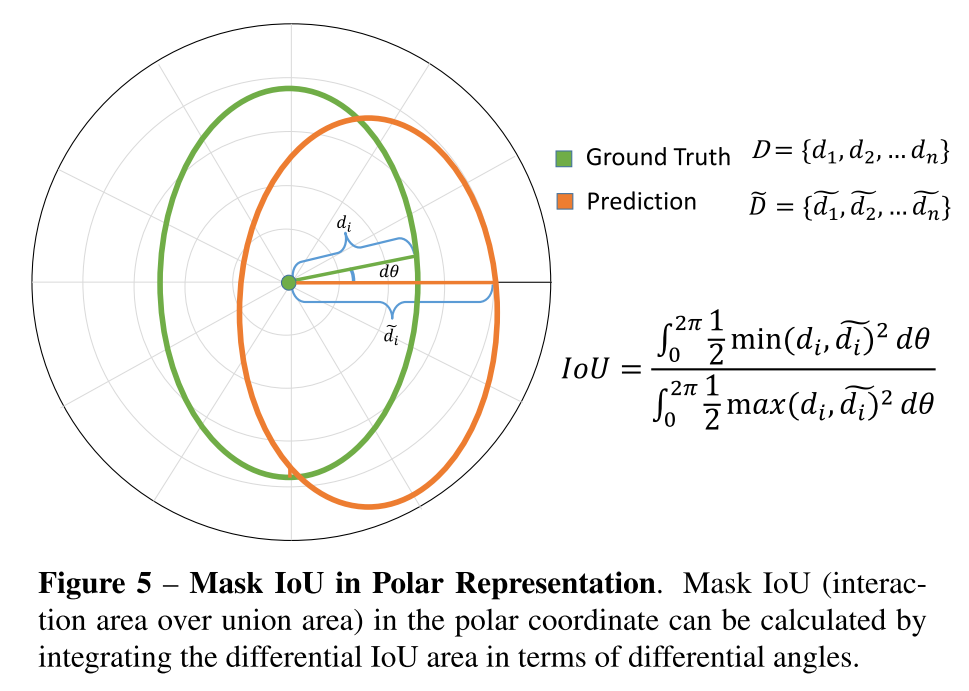
即极坐标中,两个mask交和并的面积可以表示为无数个$d\theta$ 对应的小扇形面积的积分。上述公式离散化为:
$\mathrm{IoU}=\lim _{N \rightarrow \infty} \frac{\sum_{i=1}^{N} \frac{1}{2} d_{\min }^{2} \Delta \theta_{i}}{\sum_{i=1}^{N} \frac{1}{2} d_{\max }^{2} \Delta \theta_{i}}$,当均匀取角度时,即$\Delta \theta=\frac{2 \pi}{N}$,且实验发现平方去掉对结果影响不大,因此公式简化为:
$$
\text { Polar } \mathrm{IoU}=\frac{\sum_{i=1}^{n} d_{\mathrm{min}}}{\sum_{i=1}^{n} d_{\mathrm{max}}}
$$
Polar IoU Loss就是对Polar IoU采用BCE(binary cross entropy)损失,即:
$$
\text { Polar IoU Loss }=\log \frac{\sum_{i=1}^{n} d_{\max }}{\sum_{i=1}^{n} d_{\min }}
$$
2.3 推理阶段
在推理阶段,与FCOS一样,将中心度和分类的结果相乘,作为最终的置信度得分。计算mask的最小bbox,经过IoU阈值为0.5的NMS产生最终结果。
3. 遗留问题
- 不能很好解决面包圈样式的实例。(作者指出)
- Polar IoU中的预测d的中心其实并未与真正的中心对齐,因此IoU计算的准确性受中心准确性的影响。(知乎网友)

